高性能计算服务
>
软件专区
>
最佳实践
>
LAMMPS计算热导率与Python数据后处理实践详解
LAMMPS计算热导率与Python数据后处理实践详解
目录
- 引言
- 理论背景
- LAMMPS热导率计算
- Python数据后处理
- 结果可视化与分析
- 总结与展望
引言
热导率是描述材料导热能力的关键物理量，在半导体、纳米材料、热管理等领域具有重要应用价值。本文详细介绍如何利用分子动力学模拟软件LAMMPS计算材料热导率，并结合Python进行数据后处理与可视化分析，为相关研究提供完整的技术实践指南。
目前，超算互联网提供预编译的LAMMPS 2Aug2023版本，支持一键购买使用。本文实验测试使用intelmpi2018编译的LAMMPS版本：
https://www.scnet.cn/ui/mall/detail/goods?id=1734740469651730433&resource=APP_SOFTWARE
您可以通过“我的商品”，在“应用软件”中找到或者搜索该版本商品，点击“命令行”，即可选择区域中心、命令行快速使用软件。
软件默认安装在家目录的apprepo下，环境变量默认放在软件scripts目录下的env.sh中，通过修改case文件夹的脚本文件得到我们的脚本文件。
#!/bin/bash
#SBATCH -J lammps #作业名称
#SBATCH -p tyhctest #队列名称
#SBATCH -N 2 #节点数量
#SBATCH --ntasks-per-node=32 #每节点核心数
module purge
source /work/home/bcyyy/apprepo/lammps/2Aug2023-intelmpi2018/scripts/env.sh
srun --mpi=pmi2 lmp_mpi -in in.*理论背景
热导率计算主要基于两种方法：平衡态的格林-库博公式（Green-Kubo method）和非平衡分子动力学方法（NEMD）。本实践采用NEMD方法，通过在模拟体系两端建立温度梯度，测量稳态热流来计算热导率。根据傅里叶热传导定律，热导率κ可表示为：
κ = J/(A·∇T)
其中J为热流，A为横截面积，∇T为温度梯度。
LAMMPS热导率计算
模拟体系准备
首先需要构建合适的原子模型，本例使用硅晶体作为研究对象。硅作为半导体材料，其热导率研究具有重要的应用价值。
输入文件配置
LAMMPS需要两个关键输入文件：控制脚本和原子结构文件。
控制脚本（in.heat_conductivity）
# LAMMPS热导率计算脚本
# 基本变量设置
variable simname index si # 模拟名称
variable temperature equal 300 # 系统温度（K）
variable thigh equal 280 # 热源温度（K）
variable tlow equal 320 # 热汇温度（K）
variable dt equal 0.0001 # 时间步长（ps）
variable Tdamp equal 100*${dt} # 温度阻尼参数
variable Pdamp equal 1000*${dt} # 压力阻尼参数
log log.${simname}.txt # 日志文件
# 系统初始化
units metal # 使用metal单位制
boundary p p p # 周期性边界条件
timestep ${dt} # 设置时间步长
atom_style atomic # 原子模型类型
neigh_modify every 1 delay 0 check yes # 邻居列表更新设置
neigh_modify one 10000
# 读取结构数据
read_data Si.data # 读取硅晶体结构
mass 1 28.0855 # 硅原子质量
# 区域与原子组定义
region lfixed block INF INF INF INF INF 5 units box # 左固定区域
region rfixed block INF INF INF INF 132 INF units box # 右固定区域
region thigh block INF INF INF INF 5 25 units box # 热源区域
region tlow block INF INF INF INF 112 132 units box # 热汇区域
group glfixed region lfixed # 左固定原子组
group grfixed region rfixed # 右固定原子组
group gfixed union glfixed grfixed # 所有固定原子
group gthigh region thigh # 热源原子组
group gtlow region tlow # 热汇原子组
group innt subtract all gfixed # 非固定原子组
# 势函数设置
pair_style tersoff # 选择Tersoff势
pair_coeff * * SiC.tersoff Si # 载入势参数
# 计算属性定义
compute hot_temp gthigh temp # 计算热源温度
compute cold_temp gtlow temp # 计算热汇温度
compute innt_temp innt temp # 计算非固定区域温度
# 系统能量最小化
min_style cg # 共轭梯度法
minimize 1.0e-4 1.0e-6 100 1000 # 能量最小化参数
# 系统平衡
fix 1 all npt temp ${temperature} ${temperature} ${Tdamp} iso 1.0 1.0 ${Pdamp}
fix 555 all recenter INIT INIT INIT
thermo 100000
thermo_style custom step temp press etotal lx ly lz
run 500000
unfix 1
# 第一次平衡运行
velocity all create ${temperature} 28459 rot yes dist gaussian mom yes
thermo_style custom step c_innt_temp lz ly lx pzz etotal
fix fixed1 gfixed setforce 0.0 0.0 0.0
fix NVE1 innt nve
fix Temp1 innt langevin ${temperature} ${temperature} ${Tdamp} 287859 tally yes
run 500000
unfix NVE1
unfix Temp1
# 热导率计算
reset_timestep 0
fix NVE3 innt nve
fix hot1 gthigh langevin ${thigh} ${thigh} ${Tdamp} 59804 tally yes # 热源
fix cold1 gtlow langevin ${tlow} ${tlow} ${Tdamp} 287859 tally yes # 热汇
run 1000000
# 温度分布采样
reset_timestep 0
compute KE all ke/atom # 计算原子动能
variable KB equal 8.625e-5 # 玻尔兹曼常数
variable TEMP atom c_KE/1.5/${KB} # 定义原子温度
compute BLOCKS1 all chunk/atom bin/1d z lower 0.0125 units reduced # 定义分层
fix T_PROFILE1 all ave/chunk 10 500000 5000000 BLOCKS1 v_TEMP file temp.${simname}.txt
# 输出设置
thermo_style custom step c_innt_temp c_hot_temp c_cold_temp f_hot1 f_cold1 etotal
fix ave_thermo all ave/time 10000 5 100000 f_hot1 f_cold1 file thermo.${simname}.txt
run 5000000 # 运行原子结构文件（Si.data）
LAMMPS data file for crystal
22950 atoms
1 atom types
0.0 40.7302 xlo xhi
0.0 40.7302 ylo yhi
0.0 150 zlo zhi
Masses
1 28.0855
Atoms #atomic
1 1 11.54023750 0.67883750 0.43741250
2 1 14.25558750 0.67883750 3.15276250
3 1 16.97093750 0.67883750 5.86811250
4 1 19.68628750 0.67883750 8.58346250
5 1 22.40163750 0.67883750 11.29881250
6 1 25.11698750 0.67883750 14.01416250
7 1 27.83233750 0.67883750 16.72951250
8 1 30.54768750 0.67883750 19.44486250
9 1 33.26303750 0.67883750 22.16021250
10 1 35.97838750 0.67883750 24.87556250
11 1 38.69373750 0.67883750 27.59091250
12 1 0.67883750 0.67883750 30.30626250
13 1 3.39418750 0.67883750 33.02161250
14 1 6.10953750 0.67883750 35.73696250
15 1 8.82488750 0.67883750 38.45231250
16 1 11.54023750 0.67883750 41.16766250
17 1 14.25558750 0.67883750 43.88301250
18 1 16.97093750 0.67883750 46.59836250
19 1 19.68628750 0.67883750 49.31371250
20 1 22.40163750 0.67883750 52.02906250
21 1 25.11698750 0.67883750 54.74441250
22 1 27.83233750 0.67883750 57.45976250
23 1 30.54768750 0.67883750 60.17511250
24 1 33.26303750 0.67883750 62.89046250
25 1 35.97838750 0.67883750 65.60581250
26 1 38.69373750 0.67883750 68.32116250
27 1 0.67883750 0.67883750 71.03651250
28 1 3.39418750 0.67883750 73.75186250
29 1 6.10953750 0.67883750 76.46721250
30 1 8.82488750 0.67883750 79.18256250
31 1 11.54023750 0.67883750 81.89791250
32 1 14.25558750 0.67883750 84.61326250
33 1 16.97093750 0.67883750 87.32861250
34 1 19.68628750 0.67883750 90.04396250
35 1 22.40163750 0.67883750 92.75931250
36 1 25.11698750 0.67883750 95.47466250
37 1 27.83233750 0.67883750 98.19001250
38 1 30.54768750 0.67883750 100.90536250
39 1 33.26303750 0.67883750 103.62071250
40 1 35.97838750 0.67883750 106.33606250
41 1 38.69373750 0.67883750 109.05141250
42 1 0.67883750 0.67883750 111.76676250
43 1 3.39418750 0.67883750 114.48211250
...
22945 1 12.89791250 37.33606250 123.98583750
22946 1 15.61326250 37.33606250 126.70118750
22947 1 18.32861250 37.33606250 129.41653750
22948 1 21.04396250 37.33606250 132.13188750
22949 1 23.75931250 37.33606250 134.84723750
22950 1 26.47466250 37.33606250 137.56258750模拟过程解析
- 系统准备：首先进行能量最小化。
- 热平衡：在NPT系综下平衡系统，消除初始结构中的应力。
- 热梯度建立：在系统两端分别设置热源和热汇，创建稳定的温度梯度。
- 数据采集：记录热流和温度分布数据，用于后续的热导率计算。
关于输入in文件的更多设置，可以参考官方文档指导，LAMMPS官方文档: https://docs.lammps.org/
将上述输入文件保存为in文件和data文件，并放置在同目录下，通过sbatch 脚本文件来调用资源开始仿真。
tail 一下日志查看程序运行状态
Python数据后处理
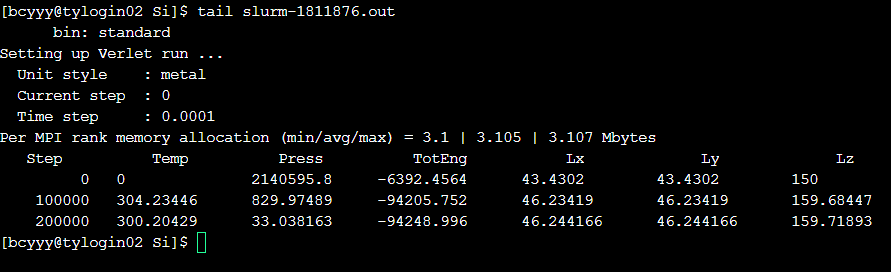
热导率计算需要处理LAMMPS输出的温度分布数据和热流数据。以下是基于Python的数据分析流程：
数据导入与预处理
python
import numpy as np
import matplotlib.pyplot as plt
# 文件路径
temp_file = "temp.si.txt" # 温度分布数据
thermo_file = "thermo.si.txt" # 热流数据
# 读取温度分布数据
with open(temp_file, 'r') as f:
lines = f.readlines()
# 跳过前4行标题行
data_lines = lines[4:]
temp_data = []
for line in data_lines:
values = line.strip().split()
# 转换为浮点数
temp_data.append([float(val) for val in values])
temp_ave = np.array(temp_data)
# 读取热流数据
with open(thermo_file, 'r') as f:
lines = f.readlines()
# 跳过前2行标题行
data_lines = lines[2:]
thermo_data = []
for line in data_lines:
values = line.strip().split()
# 转换为浮点数
thermo_data.append([float(val) for val in values])
temperature = np.array(thermo_data)热导率计算
基于非平衡分子动力学方法，热导率计算公式为：κ = (Q·L)/(A·ΔT)，其中Q为热流，L为系统长度，A为横截面积，ΔT为温度差。
python
# 参数设置
dt = 0.0001 # 时间步长（ps）
Ns = 100000 # 采样间隔
A = 4.3**2 # 横截面积（nm²）
l=14 # 长度（nm）
N_temp = len(temperature) # 时间步数
# 筛选有效温度数据（温度大于200K）
valid_temp_data = temp_ave[temp_ave[:, 3] > 200]
# 计算温度差（选取稳定区域的代表点）
temp_difference = temp_ave[12][3] - temp_ave[61][3]
print(f"温度差: {temp_difference} K")
# 计算时间序列（转换为ns单位）
t = dt * np.arange(1, N_temp + 1) * Ns / 1000
# 计算热流（能量传递率）
# 热源热流计算
Q1 = (temperature[N_temp//2-1][1] - temperature[-1][1]) / (N_temp/2) / dt / Ns
# 热汇热流计算
Q2 = (temperature[-1][2] - temperature[N_temp//2-1][2]) / (N_temp/2) / dt / Ns
# 取平均热流（单位：eV/ps）
Q = (Q1 + Q2) / 2
print(f"平均热流: {Q} eV/ps")
# 计算热导率（单位：W/mK）
G = 160 * Q *l/ A / temp_difference # 160是单位转换因子
print(f"热导率: {G} W/mK")结果可视化与分析
可视化是理解热导率计算结果的重要手段。以下代码生成三个关键图形：温度分布曲线、热源热流变化和热汇热流变化。
python
# 创建多子图布局
plt.figure(figsize=(12, 10))
# 温度分布图
plt.subplot(2, 2, 1)
plt.plot(valid_temp_data[:, 1], valid_temp_data[:, 3], 'o-', color='blue')
plt.xlabel('坐标位置')
plt.ylabel('温度 (K)')
plt.title('系统温度分布')
plt.grid(True)
# 热流对比图（原始数据）
plt.subplot(2, 2, 3)
plt.plot(temperature[:, 0]*dt/1000, temperature[:, 1], 'o-', color='red', label='热源')
plt.plot(temperature[:, 0]*dt/1000, temperature[:, 2], 'o-', color='blue', label='热汇')
plt.xlabel('时间 (ns)')
plt.ylabel('热流 (eV)')
plt.title('热流时间演化')
plt.legend()
plt.grid(True)
# 热流对比图（热汇取绝对值）
plt.subplot(2, 2, 2)
plt.plot(temperature[:, 0]*dt/1000, temperature[:, 1], 'o-', color='red', label='热源')
plt.plot(temperature[:, 0]*dt/1000, -temperature[:, 2], 'o-', color='blue', label='热汇（绝对值）')
plt.xlabel('时间 (ns)')
plt.ylabel('热流 (eV)')
plt.title('热流对称性分析')
plt.legend()
plt.grid(True)
# 优化布局并保存图像
plt.tight_layout()
plt.savefig('thermal_conductivity_analysis.png', dpi=300, bbox_inches='tight')
plt.show()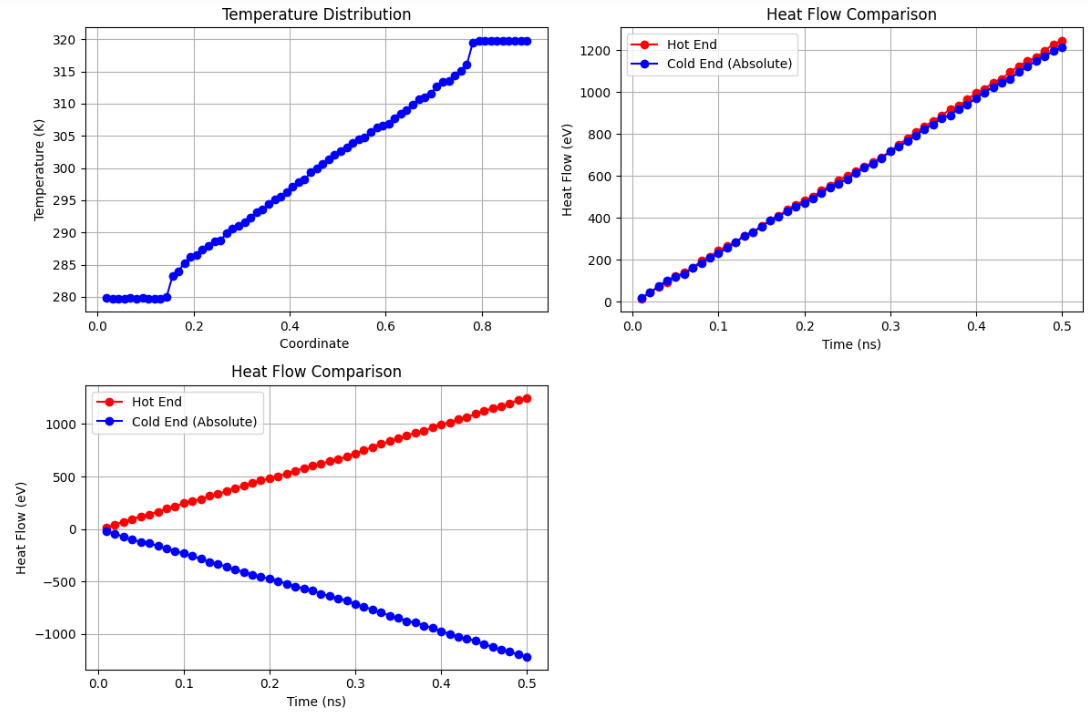
与文献中的计算结果接近
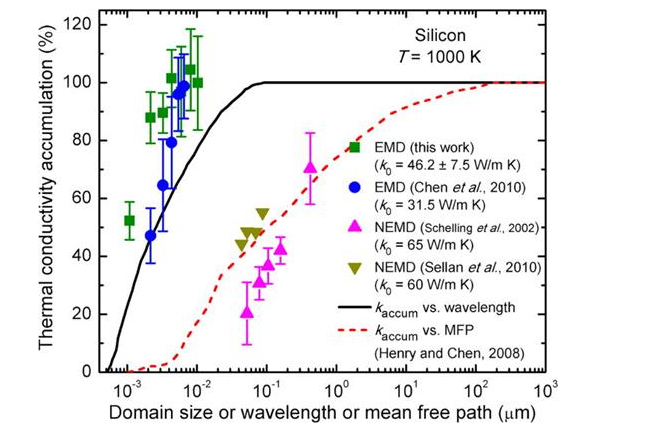
由于纳米材料有强烈的尺寸效应，大家可以进一步改变模型尺寸进行进一步研究。
总结与展望
本文详细介绍了使用LAMMPS计算材料热导率的完整流程，包括模拟体系的构建、LAMMPS输入文件的准备、高性能计算环境配置，以及基于Python的数据后处理与可视化分析。通过这一流程，研究人员可以准确评估各类材料的热传导性能，为新型高效热管理材料的设计提供指导。
参考资料：
- LAMMPS官方文档: https://docs.lammps.org/
- Zuyuan Wang, Xiulin Ruan; On the domain size effect of thermal conductivities from equilibrium and nonequilibrium molecular dynamics simulations. J. Appl. Phys. 28 January 2017; 121 (4): 044301. https://doi.org/10.1063/1.4974884
- 《计算材料学：从算法原理到代码实现》，华中科技大学出版社，2023